
MAcreateRK
Поддержите проект
- E Gold - 4337668



ПРОГРАММИРОВАНИЕ / ГЕОМЕТРИЯ / ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ


Copyright © 2007 MAcreateRK
ПРОГРАММИРОВАНИЕ

Статья - " Тригонометрия - теория и применение в программировании " от MAcreateRK
Язык - Visual Basic 6.0
содержание статьи :
- Применение тригонометрии
- Cos
- Sin
- Sin , Cos в еденичной окружности
- Основное тригонометрическое тождество
- Решение треугольников
- ArcCos
- ArcSin
- Перевод радиан в градусы и наоборот
ПРИМЕНЕНИЕ
Геометрия и тригонометрия вместе взятые , просто необходимы для хорошего программиста или для разработчика игр.
Тригонометрию можно применить в :
- Реализации вращения объекта мышю.
- Реализации вращения объекта вокруг своей оси или вокруг заданной точки.
- Создании физической модели мира , карты , человека.
- Создании вычислительных программ ( калькулятор и т.д
- Создании графических программ ( Corel Draw , Photo shop и т.д ).
- Вычислении растояния до объекта ( игра ).
- Создании различных эффектов , графических фильтров , плагинов для программ.
Еще можно найти не один десяток таких применений тригонометрии и геометрии.
COS ( косинус )
Определение :
Косинусом угла в прямоугольном треугольнике называется
Отношение противолежащего катета к гипотенузе.
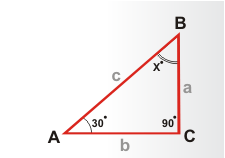
Рассмотрим косинус в треугольнике ABC :
Cos(A) = BC / AB
- BC - противолежащий катет
- AB - гипотенуза
- A - градусы
При любых значениях N : Cos(N) <= 1
это мы разберем в разделе " Sic , Cos в еденичной окружности ".
X = 180 - ( 30 + 90 ) т.к угол C - прямой , он свегда равен 90 градусов.
X = 60 градусов
Cos(60) = 0.5 => BC равен половине гипотенузы.
SIN ( синус )
Определение :
Синусом угла в прямоугольном треугольнике называется
Отношение прилежащего катета к гипотенузе.
Рассмотрим косинус в треугольнике ABC :
Sin(A) = AC / AB
- AC - прилежащий катет
- AB - гипотенуза
- A - градусы
Sin(30) = 0.5 => BC равен половине гипотенузы.
При любых значениях N : Sin(N) <= 1
это мы разберем в разделе " Sic , Cos в еденичной окружности ".
SIN , COS В ЕДЕНИЧНОЙ ОКРУЖНОСТИ
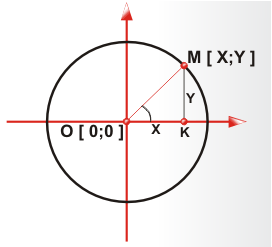
Нам дана система координат
окружность с радиусом OM
и центром в точке O [ 0;0 ]
Обозначение O [ 0;0 ] :
"О" - название точки
[ 0 - позиция по X
0 ] - позиция по Y
OM - радиус окружности и
гипотенуза трейгольника OMK
OK - прилежащий катет угла MOK
MK - противолежащий катет угла MOK
Как уже упоминалось выше :
При любых значениях N : Cos(N) <= 1
или
При любых значениях N : Sin(N) <= 1
Объяснение :
Так как мы имеем "еденичную окружность" следовательно
OM = 1 ( OM - гипотенуза )
А мы все знаем или догадываемся что гипотенуза в рпямоугольном треугольнике > прилежащего и противолежащего катета следовательно :
пример_1:
K / N
( Если K <= N ) то K / N <= N
пример_2:
Cos(30) = BC / AB
AB = 1 следовательно
BC / 1 <= 1
Sin( MOK ) = отрезку Y
Cos( MOK ) = отрезку X
X - ось абсцисс
Y - ось ординат
ОСНОВНОЕ ТРИГОНОМЕТРИЧЕСКОЕ ТОЖДЕСТВО
Для записи числа в квадрате автор использует знак " * "
Для записи чвадратного корня автор использует знак "&()"
пример :
X в квадрате - X#
Корень квадратный из - &(X)
Тождество формулируется так :
Sin(A)# + Cos(A)# = 1
Выражаем Cos(A) :
Cos(A) = &(1 - Sin(A)#)
Выражаем Sin(A) :
Sin(A) = &(1 - Cos(A)#)
С помощю данного тождества мы можем найти Cos() зная Sin() или наоборот.
РЕШЕНИЕ ТРЕУГОЛЬНИКА
Процесс - "решение треугольника"
Это процесс нахождения всех сторон данного треугольника и его углов.
Автор в данном разделе приведет конкретный формулы , без их полного пояснения.
Формула площади треугольника :
( Когда нам извесны 2 стороны и угол между ними )
Площадь = 0.5 * a * b * Sin(C)
Формулы синусов :
( Когда нам известны 2 Sin и одна сторона )
a / Sin(A) = b / Sin(B)
Формула косинусов :
( Нам надо найти 3-ю сторону , а нам известны 2 стороны и уго между ними )
c# = a# + b# - 2 * a * b * Cos(C)
ArcCos ( арккосинус )
ArcCos - это функция обратная Cos
Формулу ArcCos часто применяют для получения градусов из отношения сторон треугольника.
Формула на языке Visual Basic 6.0 :
VB : Arccos (X) = Atn (-X / Sqr (-X * X + 1)) + 2 * Atn (1)
Вы получите значение в радианах , как перевести в градусы
см. раздел " Перевод радиан в градусы и наоборот ".
ArcSin ( арксинус )
ArcSin - это функция обратная Sin
Формулу ArcSin часто применяют для получения градусов из отношения сторон треугольника.
Формула на языке Visual Basic 6.0 :
VB : Arcsin (X) = Atn (X / Sqr (-X * X + 1))
Вы получите значение в радианах , как перевести в градусы
см. раздел " Перевод радиан в градусы и наоборот ".
ПЕРЕВОД РАДИАН В ГРАДУСЫ И НАОБОРОТ
Допустим что R - это число в радианах.
Допустим что G - это число в градусах.
R = G * 180 / 3.141 ( мы градусы переводим в радианы )
G = R * 3.141 / 180 ( мы из радиан переводим в градусы)
Удачного программирования - MAcreateRK